See how a Tower of Hanoi of 4 and 5 disks is solved

• Tower of Hanoi of 4 

• Tower of Hanoi of 5

Java Program to Implement Doubly Linked List

The Difference Between Encoding, Encryption, and Hashing

Encoding is often confused with encryption and hashing. They are not the same. But before I go into the differences, I'll first mention the similarities:

1. All three transform data into another format.
2. Both encoding and encryption are reversible, unlike hashing.

And now the differences:

Encoding

The purpose of encoding is to transform data so that it can be properly (and safely) consumed by a different type of system, e.g. binary data being sent over email, or viewing special characters on a web page. The goal is not to keep information secret, but rather to ensure that it's able to be properly consumed.

Encoding transforms data into another format using a scheme that is publicly available so that it can easily be reversed. It does not require a key as the only thing required to decode it is the algorithm that was used to encode it.

Examples: ASCII, Unicode, URL Encoding, Base64

Encryption

The purpose of encryption is to transform data in order to keep it secret from others, e.g. sending someone a secret letter that only they should be able to read, or securely sending a password over the Internet. Rather than focusing on usability, the goal is to ensure the data cannot be consumed by anyone other than the intended recipient(s).

Encryption transforms data into another format in such a way that only specific individual(s) can reverse the transformation. It uses a key, which is kept secret, in conjunction with the plaintext and the algorithm, in order to perform the encryption operation. As such, the ciphertext, algorithm, and key are all required to return to the plaintext.

Examples: AES, Blowfish, RSA

Hashing

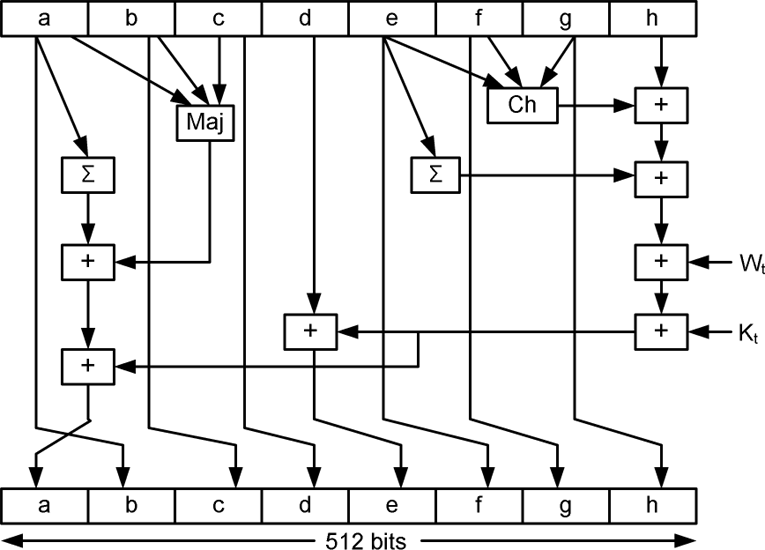
Hashing serves the purpose of ensuring integrity, i.e. making it so that if something is changed you can know that it's changed. Technically, hashing takes arbitrary input and produce a fixed-length string that has the following attributes:

1. The same input will always produce the same output.
2. Multiple disparate inputs should not produce the same output.
3. It should not be possible to go from the output to the input.
4. Any modification of a given input should result in drastic change to the hash.

Hashing is used in conjunction with authentication to produce strong evidence that a given message has not been modified. This is accomplished by taking a given input, hashing it, and then encrypting the sent hash with the recipient's public key.

When the recipient opens the message with their private key they then hash the message themselves and compare it to the hash that was given encrypted by the sender. If they match it is an unmodified message.

Examples: SHA-3, MD5 (Now obsolete), etc.

Summary

• Encoding is for maintaining data usability and can be reversed by employing the same algorithm that encoded the content, i.e. no key is used.
• Encryption is for maintaining data confidentiality and requires the use of a key (kept secret) in order to return to plaintext.
• Hashing is for validating the integrity of content by detecting all modification thereof via obvious changes to the hash output.

Hashing

Hashing is the transformation of a string of characters into a usually shorter fixed-length value or key that represents the original string. Hashing is used to index and retrieve items in a database because it is faster to find the item using the shorter hashed key than to find it using the original value. It is also used in many encryption algorithms.

As a simple example of the using of hashing in databases, a group of people could be arranged in a database like this:

Abernathy, Sara Epperdingle, Roscoe Moore, Wilfred Smith, David (and many more sorted into alphabetical order)

Each of these names would be the key in the database for that person's data. A database search mechanism would first have to start looking character-by-character across the name for matches until it found the match (or ruled the other entries out). But if each of the names were hashed, it might be possible (depending on the number of names in the database) to generate a unique four-digit key for each name. For example:

7864 Abernathy, Sara 9802 Epperdingle, Roscoe 1990 Moore, Wilfred 8822 Smith, David (and so forth)

A search for any name would first consist of computing the hash value (using the same hash function used to store the item) and then comparing for a match using that value. It would, in general, be much faster to find a match across four digits, each having only 10 possibilities, than across an unpredictable value length where each character had 26 possibilities.

The hashing algorithm is called the hash function-- probably the term is derived from the idea that the resulting hash value can be thought of as a "mixed up" version of the represented value. 

In addition to faster data retrieval, hashing is also used to encrypt and decrypt digital signatures (used to authenticate message senders and receivers). The digital signature is transformed with the hash function and then both the hashed value (known as a message-digest) and the signature are sent in separate transmissions to the receiver. Using the same hash function as the sender, the receiver derives a message-digest from the signature and compares it with the message-digest it also received. (They should be the same.) 

The hash function is used to index the original value or key and then used later each time the data associated with the value or key is to be retrieved. Thus, hashing is always a one-way operation. There's no need to "reverse engineer" the hash function by analyzing the hashed values. In fact, the ideal hash function can't be derived by such analysis. A good hash function also should not produce the same hash value from two different inputs. If it does, this is known as a collision. A hash function that offers an extremely low risk of collision may be considered acceptable.

Here are some relatively simple hash functions that have been used:

• Division-remainder method: The size of the number of items in the table is estimated. That number is then used as a divisor into each original value or key to extract a quotient and a remainder. The remainder is the hashed value. (Since this method is liable to produce a number of collisions, any search mechanism would have to be able to recognize a collision and offer an alternate search mechanism.)
• Folding method: This method divides the original value (digits in this case) into several parts, adds the parts together, and then uses the last four digits (or some other arbitrary number of digits that will work ) as the hashed value or key.
• Radix transformation method: Where the value or key is digital, the number base (or radix) can be changed resulting in a different sequence of digits. (For example, a decimal numbered key could be transformed into a hexadecimal numbered key.) High-order digits could be discarded to fit a hash value of uniform length.
• Digit rearrangement method: This is simply taking part of the original value or key such as digits in positions 3 through 6, reversing their order, and then using that sequence of digits as the hash value or key.

There are several well-known hash functions used in cryptography. These include the message-digest hash functions MD2, MD4, and MD5, used for hashing digital signatures into a shorter value called a message-digest, and the Secure Hash Algorithm (SHA), a standard algorithm, that makes a larger (60-bit) message digest and is similar to MD4. A hash function that works well for database storage and retrieval, however, might not work as for cryptographic or error-checking purposes.

Bubble Sort

Bubble Sort
Pseudocode and Flowchart

BubbleSort( int a[], int n)

Begin
 for i = 1 to n-1
  sorted = true
       for j = 0 to n-1-i
                 if a[j] > a[j+1]
                 temp = a[j]
                 a[j] = a[j+1]
                 a[j+1] = temp
           sorted = false
        end for
       if sorted
         break from i loop
 end for
End


Bubble sort uses a loop (inside j loop) to travel thru’ an array comparing adjacent
values as it moves along. If an array element a[j] is greater than the element
immediately to its right a[j+1], it swaps them. The first time around, this process will
move or bubble the largest value to the end of the array. So for instance

5 3 1 9 8 2 4 7
will end up as
3 1 5 8 2 4 7 9


This process is repeated, on the second iteration, the second largest value will be
moved to the second last array position and so on.

In all, the bubble process (inside j loop) is repeated n-1 times for an array of size n.

Note for array of size 8, outside i loop repeats 7 times.
Complexity
Clearly for an array of size n, the outside loop repeats n-1 times.

To begin with the inside loop does n-1 comparisons, next time n-2 and so on. Finally
on the last iteration of the outside loop, the inside loop does 1 comparison. So on
average the inside loop does ((n-1) + 1) / 2 ≈ n/2 comparisons.

Therefore, the overall number of computation steps is n * n/2 = n2/2

Complexity of bubble sort = O(n2)